Лариса Вольницкая - Музыкальная геометрия мира - музыка и мы. Игра-эксперимент «Узел» в письмах к М.

В таком случае напряжение разряжается, успокаивается в тонике родного дома родной тональности: всё как прежде, домашние счастливы, доминанта при них, сняла корону и надела домашние тапочки. Чай-кофе-телик, тихий сон…

Нейрон тоже разряжается, сверкнув своей королевской молнией и громом. Ему тоже нужен отдых, чтобы набраться сил для новой доминанты, время на выдох и новый вдох.

Да и вообще вся наша жизнь похожа на какую-нибудь одну отдельную Тональность, одно отдельное произведение в этой отдельной Тональности: рождаемся подобно тону-тонике, музыкальной теме; стремимся к доминанте – пику своих достижений, сверкаем и успокаиваемся, выдыхаем/исчезаем. Наша земная жизнь конечна. Дискретна. У каждого из нас – свой диапазон длиною в определённое количество лет.

(В математике ты встретишь этот термин:

дискретность– от лат. discretus– « прерывистый», « разделённый»).

Подавляющее большинство музыкальных произведений – дискретны, конечны. Но практически в каждом дискретном произведении есть Пик Бесконечности – доминанта. Кульминация (самое сильное и волнующее место в произведении) всегда происходит в доминантовойтональности. А доминанта принадлежит бесконечному квинтовому пути…

Уж если кому посчастливится в жизни испытать восторг доминанты – тот, считай, зацепился крючочком за Бесконечность!

***

У нас есть ещё модели №4 и №5.

Присмотрись к ним (на следующих страницах).

…Да, они тоже воспроизводят музыкальный строй. Но уже не клавиатурой, а узлами. Геометрически!

Мажоры и миноры – параллельны, как параллельны поверхности плоской бумажной ленты.

Квинты стали пятиугольниками (ты же помнишь, что слово «квинта» означает «пять»). Древние учёные так и мыслили числа – геометрически: треугольно, квадратно, пятиугольно…

Пятиугольник – фигура дискретная (как и другие ограниченные, конечные фигуры), но сотворяется он в нашем случае из непрерывной (непрерывно текущей, словно поток – поток звуковых волн и времени) ленты, которая в принципе может длиться бесконечно (если включить воображение).

В этих моделях дискретность и непрерывность встретились!

Благодаря… узлу.

Модель №4:

Правые узлы (лента вяжется в узел слева направо) – квинты, идущие вверх – диезные тональности. Пятиугольники вершинами вверх означают явление повышения, «диезность». (На модели – красные вершины.)

Левые узлы (лента вяжется в узел зеркально: справа налево) – квинты, идущие вниз – бемольные тональности. Пятиугольники вершинами вниз означают явление понижения, «бемольность». (На модели – синие вершины.)

Модель № 4 в сложенном виде (слева) и в свободном (справа).

Ниже – она же в трёх последовательных фрагментах.

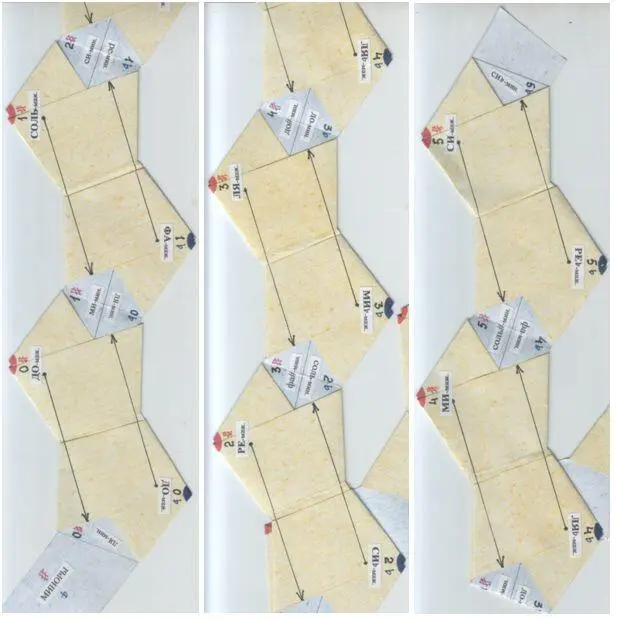
Модели автора

Между солнечными мажорными узлами проглядывают синие посредницы-медианты: миноры.

Каждому диезному мажору справасоответствует параллельный минор слева.

Каждому бемольному мажору слевасоответствует параллельный минор справа.

Коллаж автора.

Гипотенуза треугольника затем становилась горизонталью нового треугольника, – и всё повторялось так, пока не возникла галактика.

История эта геометрически воспроизводит историю с доминантой и тоникой. В роли тоники – горизонталь треугольника. Гипотенуза – в роли доминанты. Эта «доминанта» становится «тоникой» (горизонталью) нового треугольника. В нём образуется новая «доминанта»/гипотенуза, которая становится новой «тоникой»… и т.д.

Модуляции!

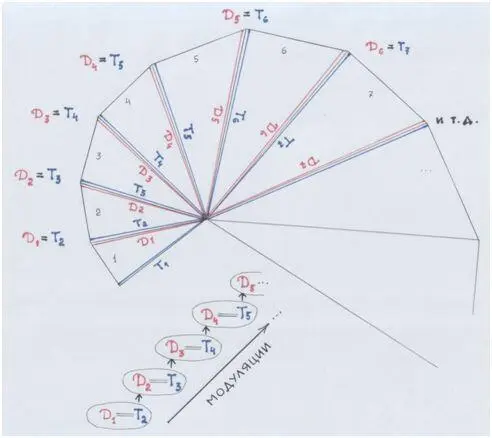
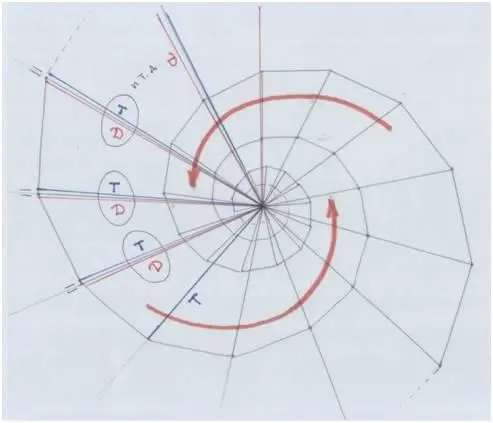
Рис. автора

В рисунке галактики ты видишь м о д у л я ц и и (изменения) треугольника. Они возможны благодаря Золотому сечению. Благодаря с а м о п о д о б и ю: все они п о д о б н ы друг другу. Это как будто один и тот же треугольник («сам») то увеличивается, то уменьшается, то возрастает, то убывает – изменяется (он вроде тот же, да не тот). Изменяется с одним и тем же коэффициентом пропорциональности.