Лариса Вольницкая - Музыкальная геометрия мира - музыка и мы. Игра-эксперимент «Узел» в письмах к М.

(Веди за этой «королевой» наблюдение на страничке ниже. Может, получится разгадать какой-то алгоритм в её движении и смене образов? – Так, для досье…)

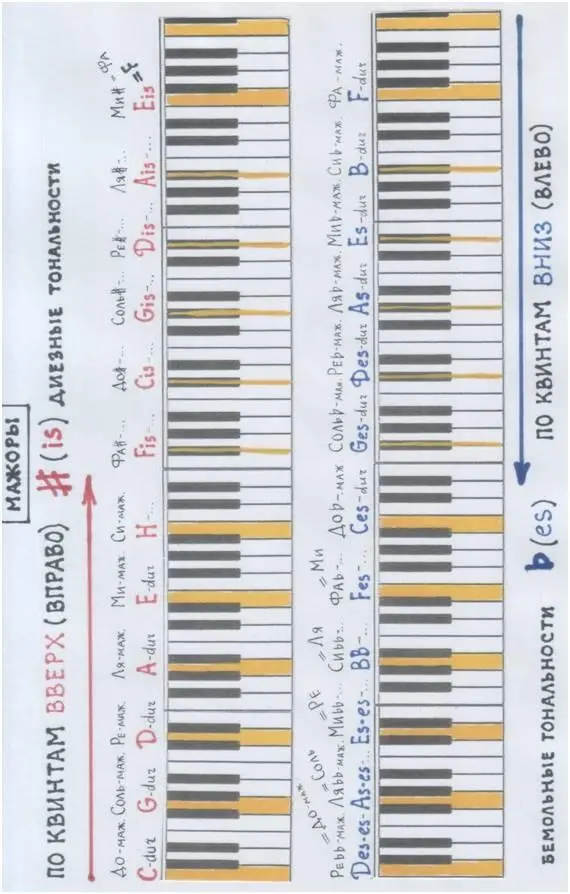
Рис. автора

Интересно, к а к д о л г о может продолжаться прогулка нашей «королевы» ( в образах тональностей, конечно же)?

…Наверное, всё зависит от длины дороги и от желания идти по ней.

Идти по солнечным лучам квинт… А если эта дорога-лестница не заканчивается длиной твоего пианино? Просто конструкторы пианино решили ограничиться охватом рук из соображений удобства?.. Разве мир звуков заканчивается там, где заканчивается пианино? Или твоя комната? Или твой город?.. Мир звуков даже не ограничивается возможностями наших, человечьих, ушей. Многие существа на Земле (животные) слышат ведь куда больше звуков, чем способны услышать мы. И для них эти звуки упорядочены подобно музыке (дельфины, например, общаются на м у з ы к а л ь н о м языке, который мы без приборов слышать неспособны; об этом – в книге Франса Де Вааля «Достаточно ли мы умны, чтобы судить об уме животных?»; и надо понимать, что сами «способности» наших приборов весьма и весьма ограниченны).

Мир звуков ведёт во Вселенную!

(Если хочешь услышать звуки Вселенной, найди на You Tube фильм «Вселенная. Звуки космоса». )

Итак, мир звуков ведёт во Вселенную…

Это однажды пронзительно ощутил и осознал Иоганн Себастьян Бах, и его музыка обрела воистину вселенский размах! И, да, он – один из первых отважных и вдохновенных Мастеров и «внедрителей» того музыкального строя, на котором держится знакомый нам мир музыки. Баха вдохновил немецкий музыкант и мыслитель в музыке Андреас Веркмейстер. А Веркмейстера вдохновили немецкий математик Генрих Грамматеус, итальянский музыкант и мыслитель Винченцо Галилей, французский математик Марен Мерсенн и фламандский математик Симон Стевин. Но самым первым открывателем знакомого нам музыкального строя считается… китайский астроном, математик и лингвист Чжу Цзайюй. Неожиданно?.. Неожиданно, что музыкой не на шутку и очень глубоко и всерьёз интересовались философы, математики, астрономы… Музыка привораживала их никак не меньше, чем к о с м и ч е с к о й значимостью, глубиной, беспредельностью, гармонией (согласованностью всего со всем, соразмерностью), стройностью.

Стройность – от слова «строй».

И да… этот строй – сияющая дорога-лестница квинт!

Ну конечно, помимо квинт есть прочие чудесные музыкальные интервалы, каждый из которых – важен (это мы поняли в связи с примой-тоникой и в связи с терцией, а также септимой («семь») и октавой само собой).

Однако тональности упрямо предпочитают «королевский» интервал для прогулок во Вселенную. Пианино – заканчивается. А музыкальный строй – нет (а звуковой вообще – тем более).

Если бы не одна «хитрость», которую придумали математики, музыкальному строю понадобилась бы клавиатура длиною в бесконечность.

Вот на следующей странице (рис.1) ты найдёшь клавиатуру, которая вознамерилась подражать бесконечности: бесконечности музыкального строя… Но её намерения так и остались незавершёнными. Ты же догадываешься, почему…

И всё-таки взгляни.

А теперь – о «хитрости» математиков.

Ты же помнишь про Мёбиуса и его ленту? «Мёбиус замкнул бесконечность в кольцо», – помнишь это высказывание?

Рассмотри модели на следующей странице. Мысленно «погуляй» по солнечным квинтам клавиатуры.

…Бесконечно?

Бесконечно можно гулять?

Эта «хитрость» музыкального строя, конечно же, была хорошо известна Баху. В его «Музыкальном приношении» (подарке) прусскому королю ФридрихуII (король тоже был музыкантом!) есть одно б е с к о н е ч н о е произведение – Модулирующий канон. Его музыкальная тема «прогуливается» бесконечно по кольцу тональностей.

«И пусть слава короля растёт по мере того как восходит модуляция!» – вот что сказал Бах, вручая королю свой подарок. (Другая интерпретация: «Пусть слава короля возрастает так же бесконечно!»)

Так что же такое эта загадочная «модуляция», приравненная к королевской славе?

…Ага, у нас, кажется, наклёвывается новый материальчик для «Досье на тональности»: что они поделывают, чем занимаются, как себя ведут…

Модель № 1. Бесконечность квинт. Клавиатура-кольцо: тоже бесконечность. Модели автора.