Какую точность можно получить этим путем, видно из слов знаменитого французского астронома прошлого века Франсуа Араго. В своей «Общепонятной астрономии» (1849) он писал:
«Посмотрим, с какою точностью возможно, пользуясь цифрами π, вычислить длину окружности, радиус которой равен среднему расстоянию Земли от Солнца (150 000 000 км).
«Если для π взять 18 цифр, то ошибка на одну единицу в последней цифре вовлечет за собой в длине вычисляемой окружности погрешность в 0,0003 миллиметра; это гораздо меньше толщины волоса. [2] «А площадь этого круга, — говорит Араго в другом месте книги, — можно вычислить с точностью до величины пространства, занимаемого мельчайшей пылинкой».

«Мы взяли 18 цифр π. Легко представить себе, какую невообразимо малую погрешность сделали бы, при огромности вычисляемой окружности, если бы воспользовались для π всеми известными его цифрами.
«Из сказанного ясно, как заблуждаются те, которые думают, будто науки изменили бы свой вид, и их применения много выиграли бы от нахождения точного π, если бы оно существовало».
Итак, даже для астрономии, — науки, прибегающей к наиболее точным вычислениям, — не требуется вполне точного решения квадратуры круга.

1. В старину при определении площади круглого участка землемеры часто поступали так: считали круг равновеликим квадрату, периметр которого равен длине окружности измеряемого участка. Какую относительную ошибку (в процентах) они при этом делали, если принять π=3,14? (Этот способ восходит к временам древнего Египта; он указан, наряду с другими, в папирусе Ринда. В средние века он был широко распространен также в Европе).
2. В древней египетской рукописи (в «папирусе Ринда») находим следующее правило для определения площади круга: она равна площади квадрата, сторона которого составляет 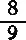 диаметра круга. Определите относительную ошибку такого расчета в %%, принимая π=3,14.
диаметра круга. Определите относительную ошибку такого расчета в %%, принимая π=3,14.
3. У нас встарину употреблялся сходный с древнеегипетским (см. предыдущую задачу) прием вычисления площади круга, рекомендуемый старинными русскими руководствами по землемерному делу площадь круга приравнивалась площади квадрата со сторонами равными 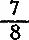 диаметра. Какой способ точнее — этот или древнеегипетский?
диаметра. Какой способ точнее — этот или древнеегипетский?
4. Валлис нашел (1656 г.) для вычисления π следующий ряд

и т. д.
Лейбниц вывел (1674) такое равенство:
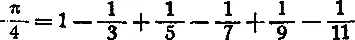
Почему этими равенствами нельзя воспользоваться для точной квадратуры круга?
5. Индусский математик Брамагупта (VII век) предложил для π следующее приближенное выражение:
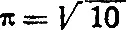
Как помощью этого выражения приближенно решить задачу о квадратуре круга?
6. Проверьте следующее приближенное равенство:
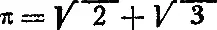
Как воспользоваться этим соотношением для приближенной квадратуры круга?
7. Проверьте приближенное равенство
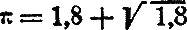
Как воспользоваться им для приближенной квадратуры круга?
8. Проверьте следующее соотношение: периметр прямоугольного треугольника с катетами в  и
и 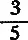 диаметра круга, приближенно равен длине окружности этого круга.
диаметра круга, приближенно равен длине окружности этого круга.
Как помощью этого соотношения приближенно решить задачу о квадратуре круга?
9. Голландский инженер Петр Меций нашел (в 1585 г.) для π легко запоминаемое выражение 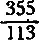 . Представив его в виде десятичной дроби, установите, сколько в ней верных цифр.
. Представив его в виде десятичной дроби, установите, сколько в ней верных цифр.
Читать дальше



 диаметра круга. Определите относительную ошибку такого расчета в %%, принимая π=3,14.
диаметра круга. Определите относительную ошибку такого расчета в %%, принимая π=3,14.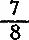 диаметра. Какой способ точнее — этот или древнеегипетский?
диаметра. Какой способ точнее — этот или древнеегипетский?
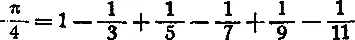
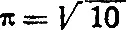
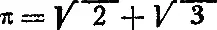
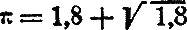
 и
и 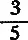 диаметра круга, приближенно равен длине окружности этого круга.
диаметра круга, приближенно равен длине окружности этого круга.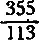 . Представив его в виде десятичной дроби, установите, сколько в ней верных цифр.
. Представив его в виде десятичной дроби, установите, сколько в ней верных цифр.




![Андрей Васильев - Квадратура круга. Том 3 [СИ]](/books/397220/andrej-vasilev-kvadratura-kruga-tom-3-si-thumb.webp)
![Андрей Васильев - Квадратура круга. Том 2 [СИ litres]](/books/407057/andrej-vasilev-kvadratura-kruga-tom-2-si-litres-thumb.webp)

![Андрей Васильев - Квадратура круга. Том 4 [СИ litres]](/books/433650/andrej-vasilev-kvadratura-kruga-tom-4-si-litres-thumb.webp)


