Коллектив авторов - Метод. Московский ежегодник трудов из обществоведческих дисциплин. Выпуск 5 - Методы изучения взаимозависимостей в обществоведении

Для того чтобы использовать (1), нужны какие‐то оценки для условных вероятностей и общего числа всех людей. «Проще» всего с величиной N S. Мы примем ее равной общему числу всех людей, когда-либо живших (и живущих сейчас) на Земле. Следует сказать, что даже эта величина нам неизвестна. Разброс составляет от 40 до 100 млрд! Например, Форстер [Foerster, 1961] использует эмпирическую формулу

где N (t) – общее число людей, живущих в момент времени t, которое, в свою очередь, отсчитывается от Рождества Христова. При этом C = 179, а T = 2027. В свою очередь, Хорнер [Hoerner, 1975] предлагает другие величины для параметров, входящих в (7): C = 200, T = 2025. Обе оценки очень неплохо согласовывались с общими демографическими данными, полученными разными способами, однако после 2000 г. появляются расхождения. Например, по Форстеру N (2002) ∼ 7,2 × 10 9человек, а по Хорнеру N (2002) ∼ 8,7 × 10 9. Вместе с тем, по официальным данным, количество народонаселения на Земле в 2002 г. только перевалило за 6 млрд и составило N (2002) ∼ 6,2 × 10 9человек. Это означает необходимость модификации (7).

Однако мы можем использовать (7) для вычисления среднего числа когда-либо живших на Земле людей. Для этого необходимо проинтегрировать N (t) от некоторого начального момента t 1 до, скажем, 2000 г. и разделить на среднюю продолжительность жизни τ. Оценки для τ варьируются от τ = 22 года (в прошлом) до τ = 42 года в наше время. Подчеркнем, что физический (или демографический) смысл величины τ таков: это среднее время смены поколений, и его можно лишь условно считать средним временем жизни. Реальное время жизни человека немного (а в развитых странах – намного) больше этого числа. Тем не менее в качестве первого приближения будем использовать эти оценки.

Полагая τ = 42 года, t 1 = − 10 4лет и интегрируя (7), получаем N total= 26 × 10 9человек для модели Форстера и N total= 29 × 10 9для модели Хорнера. Выбор τ = 22 года фактически удваивает эти величины. Если же выбрать t 1 = 10 –5лет от Р.Х., то число когда-либо живших людей оценится в 35 млрд человек при τ = 42 года или 70 млрд при τ = 22. Оценка Хорнера дает несколько большее значение. Мы не будем анализировать эти, в общем, не тривиальные проблемы, а остановимся на оценке в 60 млрд человек: N S= 6 × 10 7.

Значительно сложнее обстоит дело с величиной N L. Ситуация здесь следующая: очевидно (7) не работает при приближении к t = T, а значит, эта формула должна быть модифицирована. Приближение к особой точке приводит к так называемому демографическому переходу, феноменологическую теорию которого развивает Капица [Капица, 1996]. Отсылая заинтересованного читателя к этому обзору за подробностями, мы ограничимся выводами (не бесспорными, но это все, что у нас пока есть). Согласно Капице, точка демографического перехода отвечает 2007 г. После этого от двух от пяти десятилетий режим роста будет выходить на стационарную кривую, отвечающую максимальной численности N ∞в 15 млрд человек, причем режим будет уже устойчивым и неизменным. Эту картину и примем для оценки N L.

Прежде всего положим в (1) p S= p Lи запишем N L= N S(1 + x). Величина x определяется из простого уравнения

Смысл этого соотношения прост: в установившемся режиме с постоянным числом живущих людей N ∞общее количество живших за время t равно произведению N ∞на количество поколений, сменившихся за это время. Выражая х из (8) и подставляя в (1), получаем

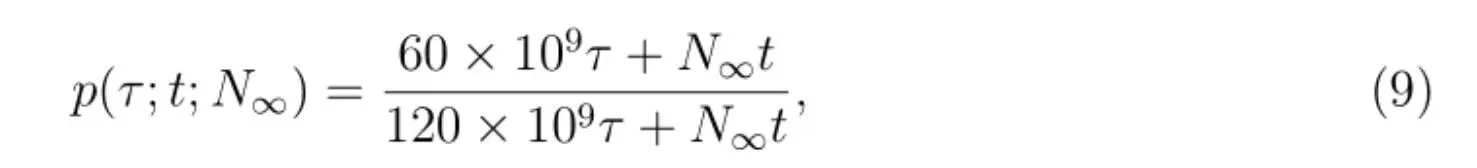
где мы ввели обозначение p (τ; t;N ∞) вместо p (S|N). Для величины τ сохраним значение в 42 года. Численные результаты выглядят следующим образом: при N ∞= 15 × 10 9человек вероятность «конца света» p (t) = p (42; t; 15 × 10 9) составляет p (20) = 0,52, p (100) = 0,62, p (200) = 0,69, p (1344) = 0,9. Время измеряется в годах. Другими словами, шансы неблагоприятного развития событий в ближайшие 40–70 лет составляют 52%, а в ближайшие 1400 лет – 90% (мы учли, что стационарный режим наступит через 20–50 лет). Если принять N ∞= 50×10 9, то оценки изменятся: p (20) = 0,58, p (100) = 0,74, p (200) = 0,83, p (403) = 0,9. То есть при таком раскладе у нас мало шансов просуществовать еще 500 лет!

В приведенных оценках существенно использовалось предположение p S= p L.

Однако верно ли оно? И можем ли мы как-то оценить эти числа при нынешнем развитии науки об обществе? Поразительно, но оказывается, это можно сделать, опять-таки используя космологию!