Владимир Карцев - Приключения великих уравнений

Так же как и уравнения Максвелла. Никакие, даже самые великие открытия не способны поколебать теорий, если они правильно отражают процессы, происходящие в мире.

По крайней мере новая теория включает старые правильные теории как крайние или частные случаи.

Так случилось с электронной теорией и уравнениями Максвелла.

Бурное развитие квантовой физики в начале нашего века натолкнуло на мысль, что максвелловы уравнения не применимы в микромире.

Простая и естественная картина непрерывного изменения электромагнитных полей, описываемая уравнениями Максвелла, здесь не может считаться полной. Ведь энергия в соответствии с гипотезой Планка должна в микромире меняться не непрерывно, а квантами, порциями!

Поэтому в 20—30-х годах нашего века был неизбежен переход максвелловой и лоренцевой теорий в новые, квантовые формы. Дирак в 1927 году, а затем Гейзенберг и Паули в 1929-м опубликовали статьи с описанием квантовой теории электромагнитного поля, где нет места непрерывности, где все величины меняются скачками и которая в случае больших объектов и расстояний переходит в старую теорию Максвелла.

Новая теория смогла объяснить ряд тонких эффектов, происходящих в микромире.

Но она внесла и много новых трудностей. Теперь оказалось, что невозможно точно измерить электромагнитное поле в точно указанной точке пространства!

Осталось в квантовой теории и прежнее противоречие лоренцевой электронной теории: энергия точечного электрона осталась бесконечной! Хитроумные способы избежать этого в рамках квантовой электродинамики привели к другому абсурду — к частице, обладающей бесконечной отрицательной массой!

Это — одна из грозовых туч над квантовой теорией электромагнитного поля. Здесь уже не «два облачка на чистом небе законченной теоретической физики», о которых говорил когда-то Дж. Дж. Томпсон. Следует учесть, что Томпсон имел в виду здесь нижеследующие «атмосферные явления»: неясность, почему электрон не падает на ядро, и странный, как тогда казалось, результат опыта Майкельсона. Мы уже знаем, какой благодатный ливень открытий и идей принесли эти «два облачка». Чем разразится грозовая туча, нависшая сейчас над квантовой теорией электромагнитного поля, пока сказать трудно. Но факт остается фактом — именно в противоречиях квантовой теории — ключ к новым открытиям в физике.

Квантовая теория электромагнитного поля неминуемо должна уступить место другой, более полной и непротиворечивой теории.

Из сказанного может показаться, что квантовая электродинамика заменила электронную теорию так же, как электронная теория заменила теорию Максвелла.

Ничто не может быть ошибочнее этого вывода. Жизнь и смерть теорий меньше всего напоминают печальную ситуацию в нашем мире, где отец дарит жизнь сыну, а сам через некоторое время исчезает из жизни, то же повторяется с сыном и внуком, и так вечно. Развитие физических идей здесь нисколько не напоминает прекрасный, но несколько жестокий процесс. Больше напоминает оно процесс деления клеток, где клетка, давшая жизнь другой, сама остается жить.

Нильс Бор писал: «…язык Ньютона и Максвелла останется языком физиков на все времена».

Ни квантовые снаряды Планка, ни буря относительности Эйнштейна не смогли сокрушить бастионы максвелловых уравнений. До сегодняшнего дня ученый, прикидывающий прохождение радиосигнала к Венере или решающий задачу «передвижения на одноколесном велосипеде по канату» — задачу удержания плазмы в «магнитной бутылке», — все они пользуются в своей работе старыми, заслуженными уравнениями Максвелла.

Но сомнения остались. Они нарастают буквально с каждым днем. Это уже не «легкие облачка», омрачавшие чистое небо физики начала века. На горизонте явно собираются свинцовые тяжелые тучи.

Собирающаяся гроза обязана своим происхождением самой, казалось бы, невинной причине — поискам красоты, полного совершенства. Недаром один великий физик не уставал говорить, что всякая физическая теория должна быть математически элегантна.

Сегодня элегантнейшая теория Максвелла уже кажется некоторым исследователям элегантной в недостаточной степени.

И дело здесь прежде всего в том, что уравнения Максвелла, как говорят математики и физики, несимметричны.

Действительно, посмотрим еще раз на уравнения Максвелла, вернее, на два из них:

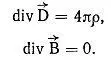
Смысл каждого из них таков: если мы возьмем ограниченную область пространства, то число электрических силовых линий (определяющее электрическое поле, D -> ), вышедших из этой области, зависит от электрического заряда ρ , располагающегося внутри нее. Чем больше заряд, тем больше D -> .