Яков Перельман - Ракетой на Луну

В старину люди верили, что возможно добраться до края земли и даже высунуть голову за небесный свод. (Этот рисунок взят из старинной книги.)

— А для меня?

— Я рассчитал, что при твоем росте ты должен видеть горизонт на расстоянии четырех километров. Завод виден тебе как раз на горизонте — значит от нас до него четыре километра. Если я пригнусь до одной высоты с тобой, то буду видеть завод, как и ты, на самом горизонте… А, вот и край луны показался!

— Я не вижу.

— Оттого, что ты ниже ростом. Для меня горизонт лежит на километр дальше, и мне видно то, чего ты еще не видишь.

Через некоторое время и я увидел верхушку светлого лунного круга, выдвинувшегося из-под горизонта.

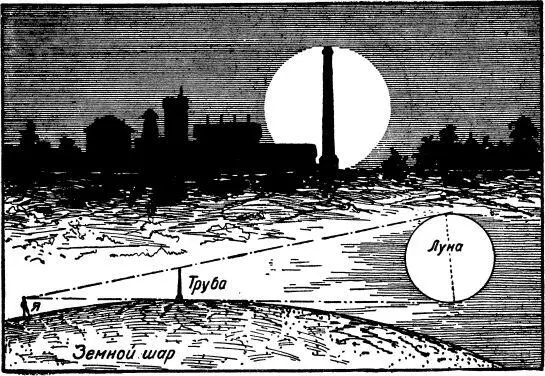
Как можно измерить величину луны, пользуясь заводской трубой

Вскоре луна выплыла вся на небо и стала большим медно-желтым кругом за черной заводской трубой. На светлом лице луны труба виднелась очень четко и помещалась как раз между краями лунного круга.

— Заводская труба и лунный поперечник кажутся отсюда одной величины, — сказал я.

— Вот именно! Для того-то я и привел тебя сюда, чтобы ты это увидел. А как ты думаешь: на самом деле луна и труба тоже одной величины?

— Луна дальше — значит, она больше.

— Во сколько раз?

— Во столько раз больше, во сколько дальше.

— Но ты ведь знаешь уже оба расстояния: и до трубы, и до луны. Сообрази же, во сколько раз лунный поперечник больше высоты трубы.

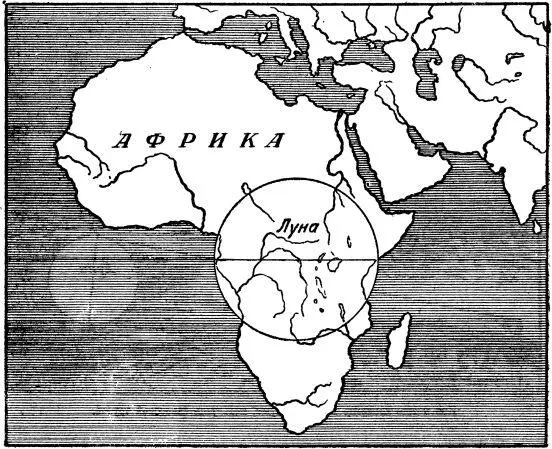
Какой величины круг луны по сравнению с материком Африки. (Надо помнить, однако, что полная поверхность лунного шара больше этого круга в четыре раза; она заключает больше квадратных километров, чем африканский материк, и немногим уступает по размерам материку Азии.)

Я начал высчитывать вслух:

— До трубы четыре километра, до луны четыреста тысяч километров. Луна дальше в сто тысяч раз. Значит, поперечник ее длиннее трубы тоже в сто тысяч раз.

— Верно! Теперь скажу тебе высоту трубы.

— Откуда ты знаешь?

— Сегодня днем я нарочно побывал на заводе и определил там ее высоту. Воткнул в землю отвесно палку и измерил ее тень. Во сколько раз тень палки короче тени трубы, во столько же раз и сама палка ниже самой трубы.

— Какой же высоты труба?

— Тридцать пять метров. И тогда же я рассчитал, что для тебя она на горизонте должна покрывать поперечник луны.

— Теперь я уж сам могу высчитать, как велик лунный поперечник, — подхватил я. — Надо тридцать пять метров умножить на сто тысяч. Сначала умножаю на одну тысячу — получаю тридцать пять тысяч метров, или тридцать пять километров. Эти тридцать пять километров множу на сто — получаю тридцать пять сотен, или три с половиной тысячи километров.

— Правильно. Вот мы и узнали длину лунного поперечника: три с половиною тысячи километров. Хороша тарелочка!

Я был так поражен этим результатом, что не поверил бы ему, если бы сам не проделал расчета. Так вот какой величины лунный шар! Его поперечник всего в четыре раза меньше земного.

— Ты убедился теперь, — сказал брат, — что луна не тарелка, а целый мир. Круг лунного шара шириной с Африку, но полная поверхность луны больше поверхности этого материка. Ученые рассчитали, что полная поверхность лунного шара по обширности лишь немного уступает Азии: в той и другой почти одинаковое число квадратных километров. А Азия, ты знаешь, огромный материк. На нем живет больше половины всего человечества, по нему протекают многоводные реки, проходят хребты высочайших гор, простираются обширные плодородные равнины и тянутся столь же обширные пустыни…

— А на луне? — спросил я.

— Ты спрашиваешь, как устроена поверхность луны? — сказал брат, когда мы направились домой. — Ученые знают об этом только то, что можно разглядеть с земли в зрительные трубы. Трубы словно приближают луну к нашим глазам, но приближают недостаточно. Самые сильные трубы показывают нам луну такою, какою видна она простому глазу с расстояния нескольких сотен километров. Много ли с такого удаления различишь?

— Что же там все-таки увидели ученые?

— При взгляде на луну в трубу, даже и не очень сильную, сразу заметно, что луна — страна горная. Поверхность лунного шара почти вся изрезана горами — целыми хребтами и множеством отдельных гор, больших и малых.