Кай Шрайбер - Честная ложь [Почему мы продолжаем верить в то, что портит нам жизнь] [litres]

Хотя мы знаем, что в принципе бывают оцинкованные монеты, у нас все же нет достоверной информации о том, в ходу ли они, и уж тем более о том, лежит ли одна из них в кармане нашего фокусника перед торговым центром. Итак, могут быть фальшивые монеты, которые всегда падают только решкой вверх, или только орлом, или как-то иначе, но не с равной долей вероятности. Использовать могут любую из них.

Примечательно, тем не менее, что человеческий мозг по-прежнему во многих сферах остается эффективнее самого лучшего компьютера и по праву считается самой сложной частью организма.

Если наблюдать за монетой, чье поведение совершенно непредсказуемо, со временем у нас все равно сложится некоторое мнение о том, падает ли она случайным образом или нет. Как нам, в этой связи, применить правило Байеса? Теперь надобно вычислять не только вероятность для двух монет, но и вероятность того, что каждая из них может быть фальшивой. Теоретически это, кажется, невозможно, ведь необходимо рассчитать бесконечное множество вещей. Айфону с такой задачей не справиться – аккумулятор раньше разрядится.

Практически же не имеет значения, выпадет решка в 20 % случаев или в 21 %. Ведь подбрасывать монету придется тысячи раз, прежде чем вообще будет заметна разница. Достаточно взять грубо диапазон в 5 %, которые будут откладываться по шкале от 0 (монета никогда не падает решкой вверх) до 100 %, когда всякий раз выпадает решка. К слову, в списке из 21 монеты есть одна подлинная, у которой в половине случаев просто обязана выпадать решка. После броска каждой из них можно рассчитать по формуле Байеса, имеем ли мы дело с таковой. В результате игры с одними монетами эта вероятность будет возрастать, с другими же – падать. В зависимости от этого сформируется и отношение к монете.

До изобретения компьютера никому и в голову не приходило применять теорему Байеса не только для отдельных случаев, но и для целого ряда одновременно происходящих событий. Но для вычислительной машины подобные расчеты не представляют никакой сложности и являются обычными. Как выяснилось, восприятие человеком или животным того или иного явления можно описать, опираясь на теорему Байеса.

О вазах, зайцах и утках

Модель восприятия, при которой наблюдатель учитывает все возможности и к каждой из них применяет теорему Байеса, в исследованиях называют «идеальный наблюдатель». Причем слово «идеальный» не значит, что наблюдатель верит всей получаемой информации. Как мы сами уже убедились, это абсолютно невозможно. В гораздо большей степени «идеальный» значит, что наблюдатель в условиях реальности со всем ее хаосом, неточностями и неоднозначностями может извлечь из представленных данных максимальную пользу.

Это возможно, если он не только находит наиболее вероятное объяснение для наблюдаемого события, но и вместе с тем получает представление о том, насколько хорошо согласовались бы с имеющимися данными прочие его интерпретации. Так получаются, например, инверсионные фигуры, вроде знаменитой иллюзии кролика-утки, описанной философом Людвигом Витгенштейном [43], или вазы Рубина [44]. Здесь конкурируют между собой два вероятных толкования одной картинки. В зависимости от условий наблюдения смотрящий склоняется в сторону одного или другого.

Однако в невинной формулировке «условия наблюдения», как и в теории относительности, заложена бомба. Она окончательно подрывает наше наивное понимание восприятия и являет собой научную основу пристрастных суждений.

Идеальный наблюдатель в действии

Еще раз вспомним теорему Байеса:

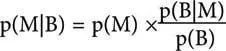
р(M|B) – вероятность того, что наше суждение верно, если некоторое наблюдаемое событие В наступило, вычисляется по двум компонентам. Во-первых, из вероятности, что это суждение соответствует истине р(М) без учета каких-либо данных, и, во-вторых, из фактора, указывающего на то, какова была бы вероятность сделанного наблюдения, если бы М было истинно. В множителе р(М), похрапывая, дремлет страшный циклоп. Без него теорема Байеса не работает и мнение идеального наблюдателя не формируется.

Для большего эффекта повторимся: то, что отражает этот множитель, – это вероятность, что наше суждение верно независимо от самого события. У нас есть для таких вероятностей практичное, короткое и многозначительное понятие. Мы называем их «предубеждениями».