Марк Абрахамс - Это невероятно! Открытия, достойные Игнобелевской премии

Затем сэндвичеведы обратились к экзотическим проблемам, лишь косвенно связанным с основной тематикой их изысканий. Примером может служить статья 1998 года под названием "Зеленые яйца и окорок" [9].

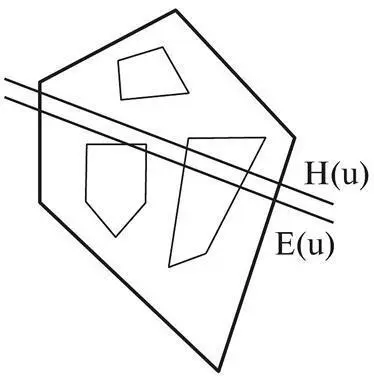
Полигональное представление ветчины и яиц. Ножевой разрез, делящий ветчину на равные по площади куски (иллюстрация к статье "Зеленые яйца и окорок").

Кто же стоял у истоков всех этих исследований, кто ввел сэндвич с ветчиной в сферу математических штудий? Данный вопрос долго оставался без ответа, пока в 2004 году не появилась статья "История раннего периода развития Теоремы о Сэндвиче с Ветчиной", авторы которой историки математики У. А. Бейер и Эндрю Зардески из Лос-Аламосской национальной лаборатории (Нью-Мексико) утверждают, что это некий еврейский ученый-теоретик по имени Гуго Штейнгауз. Бейер и Зардески отыскали "статью 1945 года, написанную польским математиком Гуго Штейнгаузом", которая "дает представление о работе Штейнгауза по разрешению проблемы сэндвича с ветчиной во время Второй мировой войны, когда он скрывался от нацистов в семье польских крестьян".

Byrnes G., Cairns G., Jessup B. (2001). Leftovers from the Ham Sandwich Theorem. American Mathematical Monthly 108 (3): 246–249. Beyer W. A., Zardecki A. (2004). The Early History of the Ham Sandwich Theorem. American Mathematical Monthly 111 (1): 58–61. Edelsbrunner H., Waupotitsch R.(1986). Computing a Ham-Sandwich Cut in Two Dimensions. Journal of Symbolic Computation 2 (2): 171178.

Zivaljevic R. T., Vrecica S. T. (1990). An Extension of the Ham Sandwich Theorem. Bulletin of the London Mathematical Society 22 (2): 183–186. Dolnikov V. L., Demidov P. G. (1992). A Generalization of the Ham Sandwich Theorem. Matematicheskie Zametki 52 (2): 27–37.

Lo Ch.-Y., Matousek J., Steiger W. (1994). Algorithms for Ham-Sand-wich Cuts. Discrete and Computational Geometry 11 (1): 433–452. Kaiser M. J., Hossaien Cheraghi S. (1998). Green Eggs and Ham. Mathematical and Computer Modeling 28 (1): 91–99.

Abbott T. G., Burr M. A., et al. Dynamic Ham-Sandwich Cuts in the Plane. Computational Geometry 42 (5): 419–428.

Steiger W., Zhao J. (2009). Generalized Ham-Sandwich Cuts. Discrete and Computational Geometry . 44 (3): 535–545.

Да, есть оптимальный (с математической точки зрения) способ налить себе вторую чашку кофе. Во всяком случае, так утверждается в статье под устрашающим названием "Рекурсивные бинарные разностные последовательности".

О том, что такой способ вообще существует, никто не подозревал до 2001 года, когда Роберт М. Ричмонд как раз и опубликовал свой нехитрый рецепт в журнале Complex Systems. В течение последующих лет, ознаменованных выпиванием по всему миру миллиардов чашек кофе, этот секрет был доступен всем желающим.

"Проблема состоит в том, что первая порция кофе, выходящая из фильтра, много крепче, нежели последняя, поэтому на дне кофейника напиток крепче, нежели тот, что находится в верхней его части, — поясняет Ричмонд. — Перемешивание жидкости в кофейнике не обеспечивает должной гомогенизации напитка. Однако ее можно добиться, если правильно наливать сваренный кофе".

Все просто. Приготовьте кофе в стеклянном кофейнике — на двоих. Теперь возьмите две чашки, назовем их А и В. Процедуру наливания в ту или иную чашку также обозначим как А и В. Затем: "Если у вас хватит терпения 4 раза налить одинаковые порции, вы можете применить следующие допустимые последовательности наливания: ААВВ, АВВА или АВАВ".

Допустим, вы избрали вариант АВВА и последовали этой схеме.

Готово. Теперь у вас две чашки кофе практически идентичного вкуса.

Ричмонд дает советы привередам: "Если вы хотите еще сильнее уменьшить эту разницу и у вас достаточно терпения, можно налить 8 порций равного объема, по 4 в каждую чашку. Число возможных последовательностей теперь составляет 35". По расчетам автора, оптимальная среди них — АВВАВААВ.

А если вы еще более разборчивы, Ричмонд готов дать совет и вам: "Можно налить 16 порций, по 8 в каждую чашку. Существует 6435 соответствующих последовательностей наливания". Автор называет лучшую: ABBABAABBAABABBA.

Аналогичные проблемы смешивания присутствуют в современной жизни повсюду. Как равномерно распределить частицы красителя, когда вы размешиваете краску? Те же проблемы относятся, как ни странно, даже к спорту: как правильно подобрать баскетбольную команду? "Рассмотрим наиболее справедливый способ, который могут применять капитан А и капитан В при наборе команд", — начинает давать очередные инструкции Ричмонд. Традиционный метод (сначала одного игрока выбирает себе А, затем B, далее они продолжают чередоваться) часто приводит к тому, что одна команда оказывается значительно сильнее другой. Следует воспользоваться кофейным методом, который, скорее всего, позволит распределить спортивный талант наиболее равномерно, насколько это вообще возможно. Капитан А начинает первый, четвертый, шестой и седьмой раунд отбора игроков, а капитан В — второй, третий, пятый и восьмой".